ABSTRACT

This paper presents an ongoing project aimed at extracting rich semantics from text. Specifically, we are interested in how semantic relations provided by a state-of-the-art semantic parser can be further combined to extract additional semantics from text. Twenty six elementary semantic relations are identified. Semantic calculus is introduced as a formalism in which various combinations of these basic relations are studied. Some results are presented showing interrelations between causation, purpose and influence relations.

KEYWORDS

Lexical semantics, natural language processing, compositional semantics.

1. INTRODUCTION

Semantic representation of text is a key element to text understanding. Several Natural Language Processing (NLP) applications would benefit from a more complete and accurate semantic representation of text. For example, a formal semantic representation of text facilitates inferences and common sense reasoning, and can greatly improve the performance of Question Answering, Information Extraction, Summarization, Machine Translation and other application systems. A semantic relation R is generally defined as a unidirectional relation between two concepts, R(x, y) describing the semantic interaction between the two concepts. In this paper, we present an ongoing research to extract enhanced semantics from text by using a formal method of combining adjacent semantic relations. This work is also useful for improving the precision of Semantic Parsers that generate automatically semantic relations from text. We identified 26 types of relations that are produced by a Semantic Parser (SP), see Table 1. No matter how accurate a Semantic Parser is, there are more semantics that can be found in text that are not explicitly expressed by the semantic relations. The reason for this is that a SP usually extracts only semantic relations between adjacent concepts in text[1]. For example, a SP can easily extract from the sentence “John is a rich man”, that John is a man, that man is rich, but it is unlikely that it will extract that John is rich.

In this paper, we outline a method, called compositional semantics, which infers new semantic relations by combining the elementary relations detected by the SP.

The proposed method consists of two parts: (1) Formal representation of semantic relations based on an entity ontology, and (2) Semantic Calculus. In the first part we formally define the domain and range for all relations, and in the second part, we study the semantics that results by pairing all 26 semantic relations. The net result is an increased number of semantic triples that provide a better understanding of the text.

2. SEMANTIC RELATIONS AND ENTITY ONTOLOGY

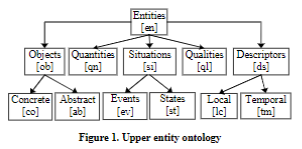
A semantic relation R(x, y) represents the semantic connectivity between concepts x and y; R is a type attribute which defines the type of the relation and x and y are the arguments. R(x, y) should be read as x is R of y. There could be any number of relation types that can be defined depending on the application. However, it is useful to carefully define a set of relations that covers most of the text semantics and use them as building blocks to express as much of text semantics as possible. Semantic relation type dictates the entity domain and range for its arguments. For example, MNR(x, y) relation has the type “MANNER” and represents that x is the manner in which y happens. MNR(x, y) is typically defined between an entity expressing a quality or manner and a situation. There have been studies in which domain and range were defined on an entity ontology [5]. This formal representation of domain and range clearly defines the sort of concepts that can be linked by a relation. In this study, we propose an upper ontology of entities for our relations, as given in Figure 1.

Using this ontology, we can define formally MANNER as MNR(x, y): [ql ᔕ st] x [si], which dictates that x can be a quality(ql) or state (st) expressing the manner in which y, a situation (si) is done. For example “quick delivery” leads to MNR(quick, delivery). Note that x and y are restricted only to the sorts of concepts indicated by that semantic relation. This formal representation has an immediate benefit on the semantic parser output since many false positives can be eliminated by checking whether or not the relation arguments satisfy the necessary constraints.

Regardless of the cardinality of the semantic relations set, these relations should be classified and organized in a thematic way depending on the sort of entities from the range and domain of the relation. This gives a formalism to the relation and its definition. This upper ontology has objects, situations, descriptors, quantities, and qualities. The objects are further divided into concrete (tangible and visible, e.g., house, singer, passport) and abstract objects (products of human reasoning, Wednesday, disease, nationality). Situations (anything that happens at a time and location) are divided into events (imply a change, e.g., hurricane, competition, run) and states (don’t imply change, e.g., being hungry). There are two types of descriptors one for local and the other one for temporal objects. A descriptor has a local or temporal part (in, on, under, etc.) followed by an object or an event. For example, “in (local part) house (concrete object)” represents a local descriptor and “during (temporal part) the party (event)” represents a temporal descriptor. Qualities represent characteristics that can be assigned to concepts. These could be quantifiable like tall, heavy or unquantifiable like difficult, sleepy, etc. Quantity represents quantitative characteristics of concepts. These could be numeral or non-numeral measurements. (e.g. 4 pounds, 2 miles, etc.).

The set of 26 relations used in this study is shown in Table 1.

As an example, we give the complete definitions of only three relations. These are Cause (CAU), Influence (INF), and Purpose (PRP):

CAU (x, y) occurs between two situations, where y would not hold if x didn’t hold. In other words, x is the cause for the occurrence of y, e.g., “I [went]y because I [read a good review]x”, “He [had to depend on himself]y, since he [was miles away from others]x”.

IFL(x, y) also occurs between two situations or objects, but captures a weaker dependency than CAU. x does not affect the occurrence of y; it affects the intensity of y, e.g., “[The war]x had an impact on [the economy]y”, “[Missing classes]x can lead to [a poor grade]y”.

PRP(x, y) holds between a situation or object and its intended purpose, e.g., “I [went to the Bahamas]y to [relax on the beach]x”, “Half of the [garage]y is used for [parking cars]x.”.

3. SEMANTIC CALCULUS

The goal of semantic calculus [4, 7] is to acquire new semantic relations using the elementary relations identified in a particular text and generally applicable semantic axioms. In this paper, we focus on axioms that combine two relations to yield a third one. Given the relations R1(x, y) and R2(y, z), we aim to obtain a new semantic relation between x and z, R3(x, z). An axiom is denoted as R1(x, y) o R2(y, z) → R3(x, z), where R1 and R2 are the premises and R3 is the conclusion. For example, the following axiom states that the parts of a whole are in the same location as the whole: LOC(x, y) o PW(y, z)→ LOC(x, z). Note that in order to combine two relations they have to share a common concept, y.

(1) CAU(x, y) o PRP(y ,z) →IFL(x, z) : This axiom reads as an event is influenced by the cause of its purpose. For example, [Being in a diet]x made John [lose weight]y. John [exercises]z to [lose weight]y. Therefore, [being in a diet]x influences [exercising]z.

(2) CAU(x, y) o PRP-1(y, z) →IFL(x, z): This axiom states that an event influences the purpose of its effect. For example, John [exercised]y yesterday because of the [good weather]x. John [exercises]y to [lose weight]z. Therefore, the [good weather]x influenced [losing weight]z.

(3) PRP(x, y) o CAU(y, z) →IFL(x, z) : This axiom indicates that an event is influenced by the purpose of its cause. For example, John [crossed carelessly]y to [get there faster]x. He [got run over by a car]z because [he crossed the street carelessly]y. Therefore, willing to [get there faster]x influenced [getting run over by a car]z.

(4) PRP-1(x, y) o CAU(y, z) →PRP-1(x, z): This axiom states that an event has as purpose the effects of its purpose. For example, They [are doing construction]x to [make wider lanes]y. [Wider lanes]y make [traffic more fluid]z. Therefore, they [are doing construction]x to make [traffic more fluid]z.

4. EVALUATION

We evaluated the performance of the axioms using manually annotated data. PRP annotation is extracted from the PropBank corpus [6], which adds predicate-argument relations to the syntactic trees of the Penn TreeBank. For CAU, we use a subset of the Penn TreeBank manually annotates with causal annotation [2]. This corpus contains pairs of verbs conjoined with the word and with temporal and causal annotation.

We found five instances of axiom 3 and thirteen of axiom 2. For all 18 instances, the inferences are valid. An example of axiom 2 is the following: “[...] by independent producers which, unlike utilities, [aren't regulated]x and therefore [don't need government approval]y to [construct new plants]z.”; CAU(x, y) o PRP-1(y, z) → IFL(x, z)

5. USE-CASES AND APPLICATIONS

There are many use-cases and applications that would benefit from compositional semantics. It may also facilitate inferring and common sense reasoning. Textual Entailment (TE) is the task of determining if the meaning of one text is entailed, i.e., can be inferred, by another [3]. The interest for TE has grown in recent years, mainly due to the fact that several NLP applications, such as Question Answering (QA), Information Extraction (IE) and Summarization can take advantage of semantic inferences to improve their performance. The RTE challenges [3] focus on the evaluation of systems for recognizing TE.

Consider the task of determining if text T entails hypothesis H:

• T: John lives in Dallas, TX.

• H: John lives in the US.

Given T, a semantic parser will output the following semantic relations: AGT(John, lives), LOC(livs, Dallas), PW(Dallas, TX). Using WordNet, we also have PW(TX, US). Given H, the same semantic parser will output AGT(John, lives), LOC(lives, US)

Using the following semantic axiom, LOC(x, y) o PW(y, z) →LOC(x, z), we can perform the following inferences:

1. LOC(lives, Dallas) o PW(Dallas, TX) → LOC(lives, TX)

2. LOC(lives, TX) o PW(TX, US) → LOC(lives, US)

And therefore we can easily conclude that T entails H by simply matching the semantic representation of T and H. Note that we could also have used the axiom LOC(x, y) o PW(y, z) o PW(z, w) → LOC(x, w).

6. CONCLUSION AND FUTURE WORK

In this paper, we have proposed a method for extracting enriched semantics from text. Currently, we are in the process of formally defining the entire set of 26 relations, specifying their domains and ranges. Analyzing the semantics of all possible combinations of a pair of relations is a tedious task, but the results are rewarding since a large number of useful inference axioms are broad to bear. Finally, another dimension of our work is to add degrees of strength to resulting axioms, namely indicating the strength of resulting semantic relations from always possible to neutral to always not possible.

7. REFERENCES

[1]Badulescu, A. and Srikanth, M. 2007. LCC-SRN: LCC’sSRN System for SemEval 2007 Tak 4. Proceedings of the Fourth International Workshop on Semantic Evaluations (SemEval-2007).
[2]Bethard, S., Corvey, W., Klingenstein,S. and Martin, J.H. 2008. Building a corpus of temporal-causal structure. In Language resources and Evaluation Conference (LREC08).
[3]Giampiccolo, D., Magnini, B., Dagan, I. and Dolan, B. 2007. The Third PASCAL Recognizing Textual Entailment Challenge. In Proceedings of the ACL-PASCAL Workshop on Textual Entailment and Paraphrasing. [4]Harabagiu, S. and Moldovan, D. 1998. Knowledge Processing on Extended WordNet. In Christian Fellbaum, editor, WordNet: an Electronic Lexical Database and Some of its Applications, pages 379-405. The MIT Press.
[5]Helbig, H. 2006. Knowledge Representation and the Semantics of Language. Springer.
[6]Palmer, M., Kingsbury, P., Gildea, D. 2005. The Propositional Bank: An Annotated Corpus of Semantic Roles. Computational Linguistics 31(1):71-106.
[7]Tatu, M. 2007. Intentions in text and Semantic Calculus. Doctoral Thesis, The University of Texas at Dallas.